Math Expression in Advanced Ladder

Topic Menu

Math Expression Overview

The Math functions allow for basic math operations as well as more advanced operations. These functions default to INT Integer - [Data Type INT] - A 16-bit signed value. Integers are used where the value of the data is expected to be in the range of -32,768 to +32,767. format but may be specified for UINT Unsigned Integer - [Data Type UINT] - A 16-bit unsigned value. Unsigned Integers are used where the value of the data is expected to be in the range of -0 (zero) to 65,535., DINT Double Integer - [Data Type DINT] - A 32-bit signed value. Double Integers are used where the value of the data is expected to be in the range of -2,147,483,648 to +2,147,483,647., UDINT Unsigned Double Integer - [Data Type UDINT] - A 32-bit unsigned value. Unsigned Double Integers are used where the value of the data is expected to be in the range of 0 (zero) to 4,294,967,296., REAL These numbers use IEEE 754-1985 format to store numbers in following ranges. 32-bit single-precision floating point (REAL) – -3.40282E+38 to +3.40282E+38 64-bit double-precision floating point (LREAL) – -1.79769E+308 to +1.7976E+308 Floating Point refers to both REAL and LREAL data types., and LREAL These numbers use IEEE 754-1985 format to store numbers in following ranges. 32-bit single-precision floating point (REAL) – -3.40282E+38 to +3.40282E+38 64-bit double-precision floating point (LREAL) – -1.79769E+308 to +1.7976E+308 Floating Point refers to both REAL and LREAL data types. formats as well. More complex functions may be found in the Advanced Math Operations toolbar.

Home > View > Project Toolbox > Math - Standard

The Expression function provides a way to combine multiple math functions into a single function. The math expression entered is calculated exactly as typed while following the standard mathematical order of operations noted by the list of supported functions that follows.

Math Parameters

Output/Result: The math expression is written such that the result location is typed first, followed by the required “=” sign, and will be equal to the outcome of the remaining expression. For Advanced Ladder Logic, only the register reference, complete with the “%” notation, may be used.
Inputs: One or more variables/registers or “hard-coded” values along with mathematical symbols. For Advanced Ladder Logic, register address references or their associated I/O name may be used; however, register references must include the “%” notation to separate them from a possible I/O name.

Type: This function will operate on INT, UINT, DINT, UDINT, REAL or LREAL data types. All parameters must be of the same type.

Note: The total length of the entire expression may not exceed 80 characters

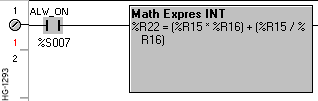
In Register Based Advanced Ladder Logic:

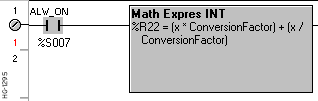
In Variable Based Advanced Ladder Logic:

Mathematical Operations Supported

The following operations are available for use with the Math Expression, listed in the order of precedence followed when solving:

ABS() (absolute value)
SQRT() (square root)
LOG() (logarithm)
EXP() (exponent, aka e(Value in parenthesis) (the base of natural logarithms))
LN() (natural logarithm)
SIN() (sine)
COS() (cosine)
TAN() (tangent)
ASIN() (arcsine or sin-1)
ACOS() (arccosine or cos-1)
ATAN() (arctangent or tan-1)
DEG() (convert Radians to Degrees)
RAD() (convert Degrees to Radians)
EXPT (Exponential, aka “to the power of”; ex. 2 EXPT 3 = 8)
* (multiplication)
/ (division)
MOD (modulo)
+ (addition)
– (subtraction)
= (required and only at beginning of expression)

Notes for Use:

It is recommended in general that a space be used between every portion of the expression with the following exceptions:

No space between open parenthesis and the next character
No space between closing parenthesis and the previous character
No space between the – sign and the number meant to be a negative number.

For maximum use of the available character limit, the subtraction operator is the only character that MUST be separated by a space from the following register/variable/value; otherwise it is considered notation that the register/variable/value is a negative number. The operational order can be forced differently from the above order by grouping with parenthesis. Parenthesis nesting may be used with no limitation other than the 80-character limit of the entire expression.

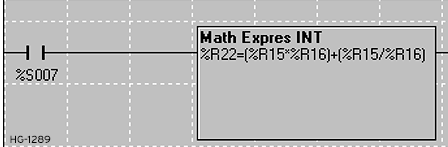
Power Flow

The Math Expression function executes immediately and entirely as soon as it receives power from the incoming rung. The resulting value is available for any other use immediately.

The Math Expression function will execute on every scan that it has received power from the incoming rung.

The Math Expression function will pass power flow to the next function on the rung unless the function overflows or underflows the data type for which it is configured, or otherwise faults (i.e. Divide by Zero).

Alert: This applies to the result or any intermediate portion of the Math Expression!

There is no need for any further functions to exist to the right of the Math Expression function on the rung. The function’s result is considered an output.

Note: Changing the I/O names of registers will not propagate through to Math Expressions that used the previous iteration of the I/O name. Errors will occur during the error check portion of the download if I/O names within a Math Expression are not associated with any register.

Note: There are three (3) possible sources of errors in a Ladder Program:

Syntax Errors - Caused by poor entry or misuse of program elements. Example: Creating a rung with only a single Input Contact (-| |- , -|/|-) on the rung.

Logical Errors - Caused by asking the controller to do something it can't or using the wrong information. Example: Triggering a timer from %I1 when the user have used %I2.

Physical Errors - Caused by misunderstanding or misuse of the hardware, especially the physical I/O points.

%R22 = (%R15 * %R16) + (%R15 / %R16)

If %R15 contains 25 and %R16 contains 5, then %R22 contains 130 after the element is completed.

Return to the Top: Math Expression in Advanced Ladder