Math - Standard in Advanced Ladder
See also: Project Toolbox for Advanced Ladder
Topic Menu
Standard Math Overview
The Math functions allow for basic math operations as well as more advanced operations. These functions default to INT![]() Integer - [Data Type INT] - A 16-bit signed value. Integers are used where the value of the data is expected to be in the range of -32,768 to +32,767. format but may be specified for UINT
Integer - [Data Type INT] - A 16-bit signed value. Integers are used where the value of the data is expected to be in the range of -32,768 to +32,767. format but may be specified for UINT![]() Unsigned Integer - [Data Type UINT] - A 16-bit unsigned value. Unsigned Integers are used where the value of the data is expected to be in the range of -0 (zero) to 65,535., DINT
Unsigned Integer - [Data Type UINT] - A 16-bit unsigned value. Unsigned Integers are used where the value of the data is expected to be in the range of -0 (zero) to 65,535., DINT![]() Double Integer - [Data Type DINT] - A 32-bit signed value. Double Integers are used where the value of the data is expected to be in the range of -2,147,483,648 to +2,147,483,647., UDINT
Double Integer - [Data Type DINT] - A 32-bit signed value. Double Integers are used where the value of the data is expected to be in the range of -2,147,483,648 to +2,147,483,647., UDINT![]() Unsigned Double Integer - [Data Type UDINT] - A 32-bit unsigned value. Unsigned Double Integers are used where the value of the data is expected to be in the range of 0 (zero) to 4,294,967,296., REAL
Unsigned Double Integer - [Data Type UDINT] - A 32-bit unsigned value. Unsigned Double Integers are used where the value of the data is expected to be in the range of 0 (zero) to 4,294,967,296., REAL![]() These numbers use IEEE 754-1985 format to store numbers in following ranges.
32-bit single-precision floating point (REAL) – -3.40282E+38 to +3.40282E+38
64-bit double-precision floating point (LREAL) – -1.79769E+308 to +1.7976E+308
Floating Point refers to both REAL and LREAL data types., and LREAL
These numbers use IEEE 754-1985 format to store numbers in following ranges.
32-bit single-precision floating point (REAL) – -3.40282E+38 to +3.40282E+38
64-bit double-precision floating point (LREAL) – -1.79769E+308 to +1.7976E+308
Floating Point refers to both REAL and LREAL data types., and LREAL![]() These numbers use IEEE 754-1985 format to store numbers in following ranges.
32-bit single-precision floating point (REAL) – -3.40282E+38 to +3.40282E+38
64-bit double-precision floating point (LREAL) – -1.79769E+308 to +1.7976E+308
Floating Point refers to both REAL and LREAL data types. formats as well. More complex functions may be found in the Advanced Math Operations toolbar.
These numbers use IEEE 754-1985 format to store numbers in following ranges.
32-bit single-precision floating point (REAL) – -3.40282E+38 to +3.40282E+38
64-bit double-precision floating point (LREAL) – -1.79769E+308 to +1.7976E+308
Floating Point refers to both REAL and LREAL data types. formats as well. More complex functions may be found in the Advanced Math Operations toolbar.
Home > View > Project Toolbox > Math - Standard
Add in Advanced Ladder 
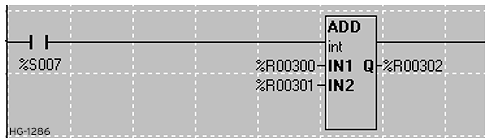
The addition function adds the two input parameters and places the result in the output parameter:
Add Parameters
-
IN1: Variable/register or static number to add to IN2.
-
IN2: Variable/register or static number to add to IN1.
-
Q: A variable/register that will contain the result of the operation. May be the same as either the IN1 or IN2 parameter to provide a self-incrementing functionality.
-
Type: This function will operate on INT, UINT, DINT, UDINT, REAL, and LREAL data types. All parameters must be of the same type.
Power Flow
The Add function executes immediately and entirely as soon as it receives power from the incoming rung. The resulting value in the Output (Q) is available for any other use immediately.
The Add function will execute on every scan that it has received power from the incoming rung.The Add function will pass power flow to the next function on the rung unless the result overflows the data type it is configured for.
There is no need for any further functions to exist to the right of the Add function on the rung. The function’s result is considered an output.
Return to the Top: Math - Standard in Advanced Ladder
Subtract in Advanced Ladder 
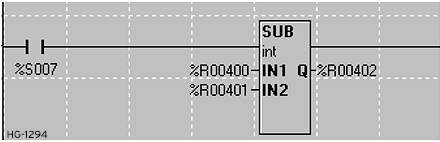
The subtraction function subtracts the IN2 parameter from the IN1 parameter and places the result in the output parameter:
Subtract Parameters
-
IN1: Variable/register or static number from which to subtract.
-
IN2: Variable/register or static number to subtract from IN1.
-
Q: A variable/register that will contain the result of the operation. May be the same as either the IN1 or IN2 parameter to provide a self-decrementing functionality.
-
Type: This function will operate on INT, UINT, DINT, UDINT, REAL, and LREAL data types. All parameters must be of the same type.
Power Flow
The Subtract function executes immediately and entirely as soon as it receives power from the incoming rung. The resulting value in the Output (Q) is available for any other use immediately.
The Subtract function will execute on every scan that it has received power from the incoming rung. The Subtract function will pass power flow to the next function on the rung unless the result underflows the data type it is configured for.
There is no need for any further functions to exist to the right of the Subtract function on the rung. The function’s result is considered an output.
Return to the Top: Math - Standard in Advanced Ladder
Multiply in Advanced Ladder 
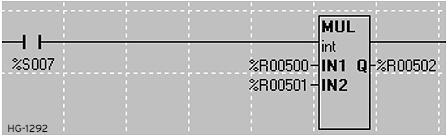
The multiplication function multiplies the input parameters and places the result in the output parameter:
Multiply Parameters
-
IN1: Variable/register or static number to multiply with IN2.
-
IN2: Variable/register or static number to multiply with IN1.
-
Q: A variable/register that will contain the result of the operation. May be the same as either the IN1 or IN2 parameter.
-
Type: This function will operate on INT, UINT, DINT, UDINT, REAL, and LREAL data types. All parameters must be of the same type.
Power Flow
The Multiply function executes immediately and entirely as soon as it receives power from the incoming rung. The resulting value in the Output (Q) is available for any other use immediately.
The Multiply function will execute on every scan that it has received power from the incoming rung. The Multiply function will pass power flow to the next function on the rung unless the result overflows the data type it is configured for.
There is no need for any further functions to exist to the right of the Multiply function on the rung. The function’s result is considered an output.
Return to the Top: Math - Standard in Advanced Ladder
Divide in Advanced Ladder 
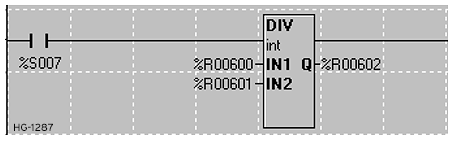
The division function divides the first input parameter by the second and places the result in the output parameter.
Divide Parameters
-
IN1: Variable/register or static number to divide using IN2.
-
IN2: Variable/register or static number with which to divide IN1.
-
Q: A variable/register that will contain the result of the operation. May be the same as either the IN1 or IN2 parameter.
-
Type: This function will operate on INT, UINT, DINT, UDINT, REAL, and LREAL data types. All parameters must be of the same type.
Usage Note: For types other than REAL and LREAL, decimal places as a result of the division will be dropped. No rounding will occur.
Power Flow
The Divide function executes immediately and entirely as soon as it receives power from the incoming rung. The resulting value in the Output (Q) is available for any other use immediately.
The Divide function will execute on every scan that it has received power from the incoming rung. The Divide function will pass power flow to the next function on the rung unless IN2 is equal to 0 (divide by zero).
There is no need for any further functions to exist to the right of the Divide function on the rung. The function’s result is considered an output.
Example: If the input values of the block are INT or DINT, then remainder is lost. For example, given the IN2 value of '5', the following is a table of some Integers Divide values:
| IN1 | IN2 | Q |
|---|---|---|
|
10 |
5 |
2 |
|
11 |
5 |
2 |
|
12 |
5 |
2 |
|
13 |
5 |
2 |
|
14 |
5 |
2 |
|
15 |
5 |
3 |
|
16 |
5 |
3 |
|
17 |
5 |
3 |
|
18 |
5 |
3 |
|
19 |
5 |
3 |
|
20 |
5 |
4 |
|
21 |
5 |
4 |
|
22 |
5 |
4 |
|
23 |
5 |
4 |
|
24 |
5 |
4 |
|
25 |
5 |
5 |
Return to the Top: Math - Standard in Advanced Ladder
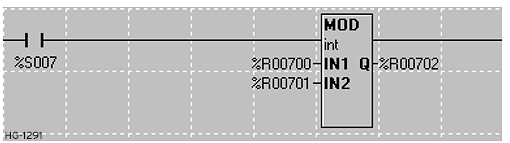
Modulo in Advanced Ladder 
The modulo function divides the first input parameter by the second, then places the remainder in the output parameter:
Modulo Parameters
-
IN1: Variable/register or static number to divide using IN2.
-
IN2: Variable/register or static number with which to divide IN1.
-
Q: A variable/register that will contain the result of the operation. May be the same as either the IN1 or IN2 parameter.
-
Type: This function will operate on INT, UINT, DINT, UDINT, REAL, and LREAL data types. All parameters must be of the same type.
Power Flow
The Modulo function executes immediately and entirely as soon as it receives power from the incoming rung. The resulting value in the Output (Q) is available for any other use immediately.
The Modulo function will execute on every scan that it has received power from the incoming rung. The Modulo function will pass power flow to the next function on the rung unless IN2 is equal to 0 (Divide by zero). There is no need for any further functions to exist to the right of the Modulo function on the rung. The function’s result is considered an output.
Performing the Modulo function on Real Numbers can appear to behave strangely if the internal workings are not understood. For example, 3.12 MOD 2.1 = 1.02. This can be better illustrated using long division:
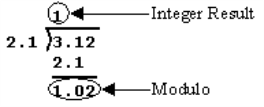
Example: This element divides IN1 by IN2 (the modulus) and places the remainder in Q. Q = remainder(IN1 / IN2)
For example, given the IN2 value of '5', the following is a table of some modulo values:
| IN1 | IN2 | Q |
|---|---|---|
|
0 |
5 |
0 |
|
1 |
5 |
1 |
|
2 |
5 |
2 |
|
3 |
5 |
3 |
|
4 |
5 |
4 |
|
5 |
5 |
0 |
|
6 |
5 |
1 |
|
7 |
5 |
2 |
|
8 |
5 |
3 |
|
9 |
5 |
4 |
|
10 |
5 |
0 |
|
11 |
5 |
1 |
|
12 |
5 |
2 |
|
13 |
5 |
3 |
|
14 |
5 |
4 |
|
15 |
5 |
0 |
Return to the Top: Math - Standard in Advanced Ladder
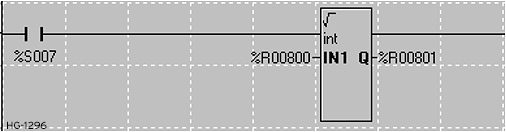
Square Root in Advanced Ladder 
Squareroot Parameters
-
IN1: Variable/register or static number of which to take the square root.
-
Q: A variable/register that will contain the result of the operation. May be the same as either the IN1 or IN2 parameter.
-
Type: This function will operate on INT, UINT, DINT, UDINT, REAL, and LREAL data types. All parameters must be of the same type.
Usage Note: For types other than REAL and LREAL, decimal places as a result of the square root function will be dropped. No rounding will occur.
Power Flow
The Square Root function executes immediately and entirely as soon as it receives power from the incoming rung. The resulting value in the Output (Q) is available for any other use immediately.
The Square Root function will execute on every scan that it has received power from the incoming rung. The Square Root function will always pass power flow as there is no error mode of the function.
There is no need for any further functions to exist to the right of the Square Root function on the rung. The function’s result is considered an output.
Example: This element figures the square root of the value in IN1 and places the result in Q.
Q = SQR(IN1)
This element has its primary use with REAL data types. This element does work with INT (16-bit) or DINT (32-bit) data, but the results of the square root function are seldom integers. The result placed in Q is truncated to the integer value.
| IN1 | Actual | Q |
|---|---|---|
|
0 |
0 |
0 |
|
1 |
1.000 |
1 |
|
2 |
1.414 |
1 |
|
3 |
1.73 |
1 |
|
4 |
2.000 |
2 |
|
5 |
2.236 |
2 |
|
6 |
2.449 |
2 |
|
7 |
2.645 |
2 |
|
8 |
2.828 |
2 |
|
9 |
3.000 |
3 |
|
10 |
3.162 |
3 |
|
11 |
3.316 |
3 |
|
12 |
3.464 |
3 |
|
13 |
3.605 |
3 |
|
14 |
3.741 |
3 |
|
15 |
3.872 |
3 |
|
16 |
4.000 |
4 |
Return to the Top: Math - Standard in Advanced Ladder
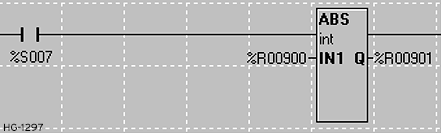
Absolute Value in Advanced Ladder 
The Absolute Value function strips the negative sign from a number, if any, and provides a positive-only equivalent value, aka the distance from zero. For a value of zero, the result is zero.
Q + |IN1|
Absolute Value Parameters
-
IN1: Variable/register or static number of which to take the absolute value.
-
Q: A variable/register that will contain the result of the operation. May be the same as either the IN1 or IN2 parameter.
-
Type: This function will operate on INT, UINT, DINT, UDINT, REAL, and LREAL data types. All parameters must be of the same type.
Power Flow
The Absolute Value function executes immediately and entirely as soon as it receives power from the incoming rung. The resulting value in the Output (Q) is available for any other use immediately.
The Absolute Value function will execute on every scan that it has received power from the incoming rung. The Absolute Value function will always pass power flow as there is no error mode of the function.
There is no need for any further functions to exist to the right of the Absolute Value function on the rung. The function’s result is considered an output.
Return to the Top: Math - Standard in Advanced Ladder